Un repaso sobre la importancia estadística

Cuando realizas un experimento o analizas datos, querrás saber si tus hallazgos son «significativos». Pero la relevancia empresarial (es decir, la importancia práctica) no siempre es lo mismo que la confianza en que un resultado no se debe únicamente al azar (es decir, la importancia estadística). Se trata de una distinción importante; desafortunadamente, significación estadística a menudo se malinterpreta y se usa mal en las organizaciones de hoy en día. Sin embargo, dado que cada vez más empresas confían en los datos para tomar decisiones empresariales críticas, es un concepto esencial que los gerentes deben entender.

Para entender mejor lo que significa realmente la significación estadística, hablé con Tom Redman, autor de Impulsado por datos: Beneficiarse de su activo empresarial más importante. También asesora a las organizaciones sobre sus programas de calidad de datos y datos.

¿Qué es la importancia estadística?

«La significación estadística ayuda a cuantificar si es probable que un resultado se deba al azar o a algún factor de interés», afirma Redman. Cuando un hallazgo es significativo, simplemente significa que puede sentirse seguro de que es real, no que simplemente tuvo suerte (o mala suerte) al elegir la muestra.

Cuando realizas un experimento, realizas una encuesta, realizas una encuesta o analizas un conjunto de datos, realizas un muestra de alguna población de interés, sin mirar todos los puntos de datos que pueda. Considere el ejemplo de una campaña de marketing. Has creado un nuevo concepto y quieres ver si funciona mejor que el actual. No puedes mostrárselo a todos los clientes objetivo, por supuesto, así que eliges un grupo de muestra.

Cuando ejecutas los resultados, descubres que quienes vieron la nueva campaña gastaron $10.17 en promedio, más que los $8.41 que gastaron los que vieron la anterior. Estos $1.76 pueden parecer una gran, y quizás importante, diferencia. Pero en realidad puede haber tenido mala suerte al dibujar una muestra de personas que no representan a la población en general; de hecho, tal vez no hubo diferencia entre las dos campañas y su influencia en los comportamientos de compra de los consumidores. Esto se llama error de muestreo, algo a lo que debes enfrentarte en cualquier prueba que no incluya a toda la población de interés.

Redman señala que hay dos factores principales que contribuyen al error de muestreo: el tamaño de la muestra y la variación en la población subyacente. El tamaño de la muestra puede ser bastante intuitivo. Piensa en lanzar una moneda cinco veces en lugar de lanzar 500 veces. Cuantas más veces des la vuelta, menos probabilidades tendrás de acabar con una gran mayoría de cabezas. Lo mismo ocurre con la importancia estadística: con tamaños de muestra más grandes, es menos probable que obtenga resultados que reflejen la aleatoriedad. En igualdad de condiciones, te sentirás más cómodo con la precisión de la diferencia de $1.76 de las campañas si mostraste la nueva a 1000 personas en lugar de solo 25. Por supuesto, mostrar la campaña a más personas cuesta más, así que tienes que equilibrar la necesidad de un tamaño de muestra más grande con tu presupuesto.

La variación es un poco más complicada de entender, pero Redman insiste en que desarrollar un sentido de la misma es fundamental para todos los gerentes que usan datos. Considera las imágenes a continuación. Cada uno expresa una posible distribución diferente de las compras de los clientes en la campaña A. En el gráfico de la izquierda (con menos variación), la mayoría de las personas gastan aproximadamente la misma cantidad de dólares. Algunas personas gastan unos cuantos dólares más o menos, pero si eliges un cliente al azar, es muy probable que se acerque bastante al promedio. Por lo tanto, es menos probable que seleccione una muestra que se vea muy diferente de la población total, lo que significa que puede confiar relativamente en sus resultados.

Compárelo con el gráfico de la derecha (con más variaciones). Aquí, las personas varían más en cuanto al gasto. El promedio sigue siendo el mismo, pero bastantes personas gastan más o menos. Si eliges un cliente al azar, es más probable que esté bastante lejos del promedio. Por lo tanto, si seleccionas una muestra de una población más variada, no puedes confiar tanto en tus resultados.

En resumen, lo importante a entender es que cuanto mayor sea la variación en la población subyacente, mayor será el error de muestreo.

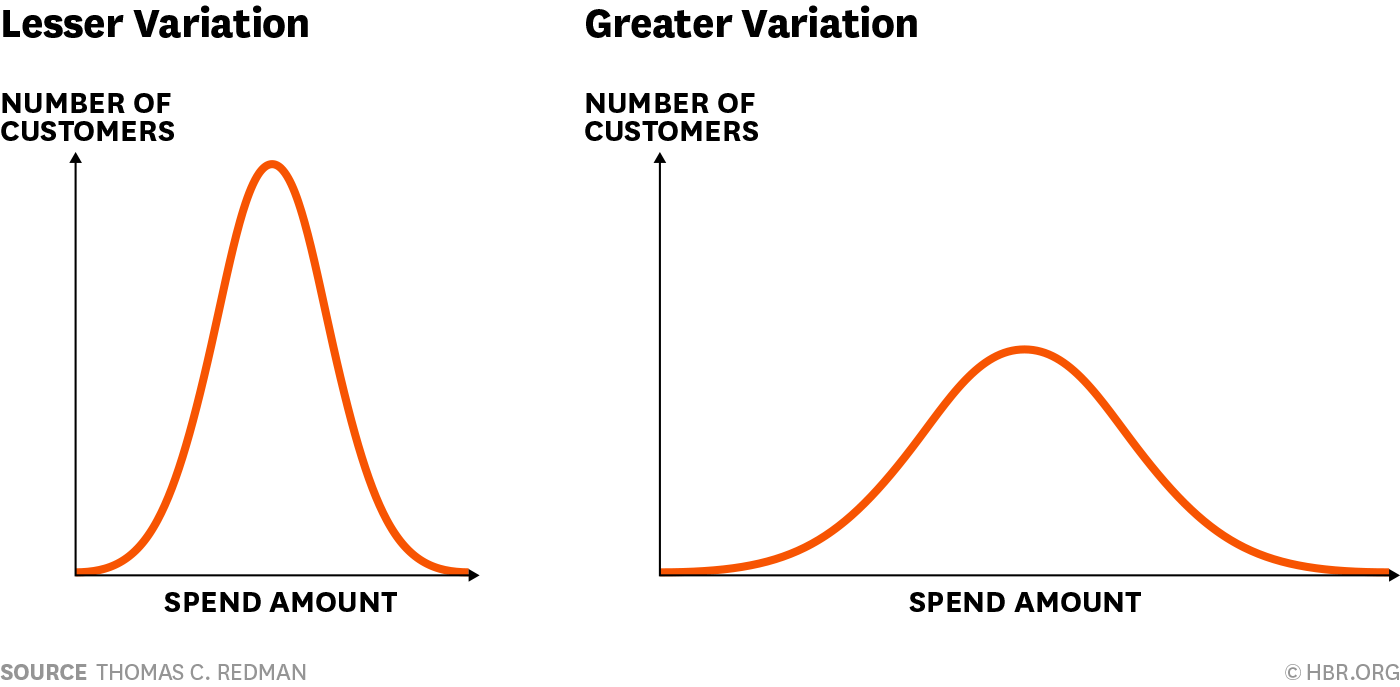
Redman aconseja que traze sus datos y haga imágenes como estas cuando analice los datos. Los gráficos le ayudarán a tener una idea de la variación, el error de muestreo y, a su vez, la importancia estadística.

Independientemente de lo que estés estudiando, el proceso para evaluar la importancia es el mismo. Empiezas por plantear una hipótesis nula, a menudo un hombre de paja que intentas refutar. En el experimento anterior sobre la campaña de marketing, la hipótesis nula podría ser «En promedio, los clientes no prefieren nuestra nueva campaña a la anterior». Antes de empezar, también debe establecer una hipótesis alternativa, como «En promedio, los clientes prefieren la nueva» y un nivel de significado objetivo. El nivel de significado es una expresión de cuán raros son sus resultados, bajo el supuesto de que la hipótesis nula es cierta. Por lo general, se expresa como un «valor p» y cuanto más bajo sea el valor p, menos probabilidades hay de que los resultados se deban únicamente al azar.

Establecer un objetivo e interpretar los valores p puede ser tremendamente complejo. Redman dice que depende mucho de lo que estés analizando. «Si estás buscando el bosón de Higgs, probablemente quieras un valor p extremadamente bajo, tal vez 0.00001», dice. «Pero si está probando si su nuevo concepto de marketing es mejor o si las nuevas brocas que su ingeniero diseñó funcionan más rápido que las brocas existentes, probablemente esté dispuesto a tomar un valor más alto, tal vez hasta 0,25».

Tenga en cuenta que en muchos experimentos comerciales, los gerentes omiten estos dos pasos iniciales y no se preocupan por la importancia hasta después de que se obtienen los resultados. Sin embargo, es una buena práctica científica hacer estas dos cosas con anticipación.

Luego recopila sus datos, traza los resultados y calcula estadísticas, incluido el valor p, que incorpora la variación y el tamaño de la muestra. Si obtiene un valor p más bajo que su objetivo, entonces rechaza la hipótesis nula a favor de la alternativa. De nuevo, esto significa que la probabilidad es pequeña de que los resultados se deban únicamente al azar.

¿Cómo se calcula?

Como gerente, es probable que nunca calcule la significación estadística usted mismo. «La mayoría de los buenos paquetes estadísticos reportarán la importancia junto con los resultados», dice Redman. También hay una fórmula en Microsoft Excel y varias otras herramientas en línea que lo calcularán por ti.

Aun así, es útil conocer el proceso descrito anteriormente para comprender e interpretar los resultados. Como aconseja Redman, «los gerentes no deben confiar en un modelo que no entiendan».

¿Cómo lo usan las empresas?

Las empresas utilizan la importancia estadística para entender con qué fuerza los resultados de un experimento, una encuesta o una encuesta que han realizado deben influir en las decisiones que toman. Por ejemplo, si un gerente realiza un estudio de precios para entender cuál es la mejor manera de poner precio a un nuevo producto, calculará la importancia estadística (muy probablemente con la ayuda de un analista) para saber si los resultados deberían afectar al precio final.

¿Recuerdas que la nueva campaña de marketing anterior produjo un aumento de $1.76 (más del 20%) en las ventas promedio? Sin duda, tiene un significado práctico. Si el valor p llega a 0.03, el resultado también es estadísticamente significativo y debes adoptar la nueva campaña. Si el valor p llega a 0.2, el resultado no es estadísticamente significativo, pero dado que el aumento es tan grande, probablemente continúe, aunque quizás con un poco más de precaución.

Pero, ¿qué pasaría si la diferencia fuera solo unos pocos centavos? Si el valor p llega a 0.2, te quedarás con tu campaña actual o explorarás otras opciones. Pero aunque tuviera un nivel de significación de 0.03, el resultado probablemente sea real, aunque bastante pequeño. En este caso, tu decisión probablemente se basará en otros factores, como el costo de implementar la nueva campaña.

Estrechamente relacionada con la idea de un nivel de significación está la noción de un intervalo de confianza. Tomemos el ejemplo de una encuesta política. Supongamos que hay dos candidatos: A y B. Los encuestadores realizan un experimento con 1000 «votantes probables». El 49% de la muestra dice que votará por A y el 51% dice que votará por B. Los encuestadores también informaron un margen de error de +/- 3%.

«Técnicamente», dice Redman, «el 49% +/ -3% es un 'intervalo de confianza del 95% 'para la verdadera proporción de votantes A en la población». Desafortunadamente, dice, la mayoría de la gente interpreta esto como «hay un 95% de posibilidades de que el verdadero porcentaje de A esté entre el 46% y el 52%», pero eso no es correcto. En cambio, dice que si los encuestadores tuvieran que hacer el resultado muchas veces, el 95% de los intervalos construidos de esta manera contendrían la proporción verdadera.

Si tu cabeza da vueltas en esa última oración, no estás solo. Como dice Redman, esta interpretación es «increíblemente sutil, demasiado sutil para la mayoría de los gerentes e incluso para muchos investigadores con títulos avanzados». Dice que la interpretación más práctica de esto sería «No se emocione demasiado de que B tenga un candado en las elecciones» o «B parece tener una ventaja, pero no es una estadísticamente significativa». Por supuesto, la interpretación práctica sería muy diferente si el 70% de los votantes probables dijeran que votarían por B y el margen de error fuera del 3%.

La razón por la que los gerentes se preocupan por la importancia estadística es que quieren saber qué dicen los hallazgos sobre lo que deben hacer en el mundo real. Pero «los intervalos de confianza y las pruebas de hipótesis se diseñaron para apoyar la 'ciencia', donde la idea es aprender algo que resista la prueba del tiempo», dice Redman. Incluso si un hallazgo no es estadísticamente significativo, puede ser útil para usted y su empresa. Por otro lado, cuando trabajas con grandes conjuntos de datos, es posible obtener resultados estadísticamente significativos pero prácticamente sin sentido, como que un grupo de clientes tiene un 0,000001% más de probabilidades de hacer clic en la Campaña A que en la Campaña B. Así que en lugar de obsesionarse con si tus hallazgos son exactamente bien, piense en las implicaciones de cada hallazgo para la decisión que espera tomar. ¿Qué haría de manera diferente si el hallazgo fuera diferente?

¿Qué errores cometen las personas cuando trabajan con significación estadística?

«La importancia estadística es un concepto resbaladizo y, a menudo, se malinterpreta», advierte Redman». No me topo con muchas situaciones en las que los gerentes necesiten entenderlo en profundidad, pero necesitan saber cómo no utilizarlo mal».

Por supuesto, los científicos de datos no tienen el monopolio de la palabra «significativo» y, a menudo, en las empresas, se utiliza para indicar si un hallazgo es estratégicamente importante. Es recomendable utilizar un lenguaje lo más claro posible cuando se habla de los hallazgos de datos. Si desea analizar si el hallazgo tiene implicaciones para su estrategia o decisiones, está bien usar la palabra «significativo», pero si quiere saber si algo es estadísticamente significativo (y debería querer saberlo), sea preciso en su idioma. La próxima vez que veas los resultados de una encuesta o experimento, pregunta sobre la importancia estadística si el analista no lo ha informado.

Recuerde que las pruebas de significación estadística le ayudan a tener en cuenta los posibles errores de muestreo, pero Redman dice que lo que suele ser más preocupante es la error de no muestreo: «Los errores no relacionados con el muestreo implican cosas en las que los protocolos experimentales y/o de medición no se realizaron de acuerdo con el plan, como las personas que mienten en la encuesta, la pérdida de datos o se cometen errores en el análisis». Aquí es donde Redman ve resultados más preocupantes. «Hay muchas cosas que pueden suceder desde el momento en que planificas la encuesta o el experimento hasta el momento en que obtienes los resultados. Me preocupa más si los datos sin procesar son confiables que con cuántas personas con las que hablaron», dice. Los datos limpios y el análisis cuidadoso son más importantes que la importancia estadística.

Ten en cuenta siempre la aplicación práctica del hallazgo. Y no te obsesiones demasiado en establecer un intervalo de confianza estricto. Redman dice que existe un sesgo en la literatura científica de que «un resultado no se podía publicar a menos que alcanzara una p = 0.05 (o menos)». Pero para muchas decisiones, como qué enfoque de marketing utilizar, necesitarás un intervalo de confianza mucho menor. En los negocios, dice Redman, a menudo hay criterios más importantes que la significación estadística. La pregunta importante es: «¿El resultado se destaca en el mercado, aunque solo sea por un breve período de tiempo?»

Como dice Redman, los resultados solo le dan tanta información: «Estoy a favor de usar las estadísticas, pero siempre lo comparo con buen juicio».

— Escrito por Amy Gallo